نقاط حادثه خیز و روش‌های شناسایی آن‌ها

 نقاط حادثه خیز به نقاطی از جاده اطلاق می‌شود که نرخ تصادفات آن‌ها از حد متوسط بالاتر باشد(Lynn B. Meuleners, 2008). طبق تحقیقات انجام شده، شناسایی، تحلیل و مدیریت نقاط حادثه خیز روشی موثر در کاهش خسارات و تلفات رانندگی می‌باشد.
بنابراین شناسایی صحیح نقاط حادثه خیز در ایمن سازی راه‌ها، حایز اهمیت است، در غیر این صورت بودجه و انرژی زیادی به هدر رفته و نقاط حادثه خیز جاده نیز به قوت خود باقی مانده و تلفات جاده ای به روال سابق ادامه می‌یابند. در ادامه روش‌های تعیین نقاط حادثه خیز معرفی و تشریح شده اند.

1-1 نمایش نقشه ی تصادفات

نقشه ی تصادفات، نحوه ی پراکندگی تصادفات را بر روی نقشه نمایش می دهد. با مطالعه ی این نقشه می توان نقاط پر خطر جاده ای را به صورت تقریبی شناسایی نمود. از مزایای این روش می توان به سادگی و سهولت آن در تعیین نقاط حادثه خیز اشاره نمود.
در کل این روش، متدی تقریبی برای تعیین مقاطع و نقاط حادثه خیز بوده و برای شبکه راه های گسترده با تصادفات متعدد، چندان کارایی ندارد. علاوه بر آن در صورت متمرکز بودن تصادفات در محل های خاص امکان پوشش تصادفات بر روی یکدیگر و دیده نشدن تجمع تصادفات وجود دارد.

1-2 روش فرکانس تصادفات

این روش از تعداد وقوع تصادفات در واحد زمان برای مکان های خاص جهت تعیین میزان ایمنی آن قسمت استفاده نموده و مکان‌هایی با فرکانس تصادفات بیش از حد مورد نظر به عنوان نقاط حادثه خیز جاده شناسایی می‌شوند(Kowtanapanich, 2007). کارایی این روش بیشتر برای شبکه ی راه های شهری بوده که فرکانس تصادفات در تقاطع ها و یا مناطق خاص شمرده شده و نقاط پر تصادف جهت ایمن سازی شناسایی می شوند.

1-3 روش تراکم تصادفات

تراکم تصادفات از تعداد تصادفات به ازای یک طول واحد برای هر بخش جاده محاسبه می‌شود. بخش‌هایی از جاده با تراکم تصادفات بیش از حد مورد انتظار به عنوان نقاط حادثه خیز شناسایی می‌شوند(Kowtanapanich, 2007).
این روش می تواند به سادگی مقاطع حادثه خیز را شناسایی نماید. از معایب این روش می توان به در نظر نگرفتن شدت تصادفات و همچنین تشخیص مقاطع با ترافیک عبوری بالا به عنوان نقاط حادثه خیز اشاره نمود.

1-4 روش نرخ تصادفات(Accident Rate Method)

نرخ تصادفات از تعداد تصادفات به ازای طول واحد از راه و تعداد واحدی وسایل نقلیه که در مسیر حرکت نموده اند، محاسبه می شود. مثلاً تعداد تصادفات برای یک میلیون وسیله ی نقلیه به ازای هر کیلومتر از جاده محاسبه شده و قطعاتی از مسیر با نرخ تصادفات بیش از حد قابل قبول به عنوان نقاط پر تصادف شناسایی می‌شوند(Kowtanapanich, 2007). نرخ تصادفات محاسبه شده از این روش مقدار بسیار کوچکی خواهد بود، بنابراین معمولاً ضریبی برای نرخ تصادفات در نظر گرفته می شود تا خوانایی ارقام به دست آمده افزایش یافته و بررسی آن ها با سهولت بیشتری صورت پذیرد. نرخ تصادفات برای قسمتی از مسیر مطابق با رابطه ی 1 محاسبه می شود (Powers & Carson, 2004).

در این رابطه R نرخ تصادفات، A تعداد تصادفات در مسیر، T بازه ی زمانی وقوع تصادفات، V متوسط ترافیک عبوری سالیانه از مسیر (AADT) و L طول مسیر می باشد.
در این روش احتمال شناسایی مقاطع کم ترافیک به عنوان مقاطع حادثه خیز، بیش از سایر روش ها می باشد. بنابراین معمولاً پس از رتبه بندی مقاطع با استفاده از این روش، ترافیک عبوری مقاطع مورد بررسی قرار گرفته و نهایتاً نقاط حادثه خیز شناسایی می شوند.

1-5 روش تراکم-نرخ

روش تراکم-نرخ، ترکیبی از روش های تراکم تصادفات و نرخ تصادفات می باشد. مقاطعی که دارای نرخ تصادفات و یا ترکم تصادفات بیش از حد معینی باشند، به عنوان مقاطع حادثه خیز در نظر گرفته می شوند(Powers & Carson, 2004). در مجموع از روش های ترکیبی مانند این روش در موارد متعددی برای ارزیابی ریسک تصادفات استفاده شده است. به عنوان مثال SweRoad(Swedish Road National Consulting) از ترکیب سه روش نرخ تصادفات، فرکانس تصادفات و شدت تصادفات برای تعیین نقاط حادثه خیز در دو ایالت کشور تایلند استفاده نموده است. در این روش اگر تنها یکی از پارامتر‌های ایمنی مقطع مسیر بالاتر از مقدار مرزی باشد، آن مقطع به عنوان نقطه ی حادثه خیز شناسایی می‌شود(Kowtanapanich, 2007).

1-6 روش کنترل کیفیت

در روش کنترل کیفیت، قطعات شبکه ی راه ها بر اساس خصوصیات فیزیکی و ترافیکی طبقه بندی می شوند. مقاطعی با تراکم یا نرخ تصادفات با اختلاف زیاد از حد متوسط طبقه ی خود، به عنوان مقاطع حادثه خیز شناسایی می شوند.
کارایی مهم این روش، در تشخیص مقاطعی است که پتانسیل بالایی برای ایمن سازی از طریق اقدامات پیشگیرانه دارند. به عنوان مثال ممکن است مقاطعی به عنوان نقاط حادثه خیز شناسایی شوند ولی با توجه به میزان ترافیک عبوری از آن مقاطع و یا سایر خصوصیات فیزیکی آن ها، امکان ایمن سازی آن مقاطع وجود نداشته باشد. به همین جهت روش کنترل کیفیت حائز اهمیت ویژه بوده و می تواند مقاطع با پتانسیل مناسب برای ایمن سازی را شناسایی نماید. Hauer در توضیح این روش، مثال زیر را مطرح نموده است (Hauer, 1996).
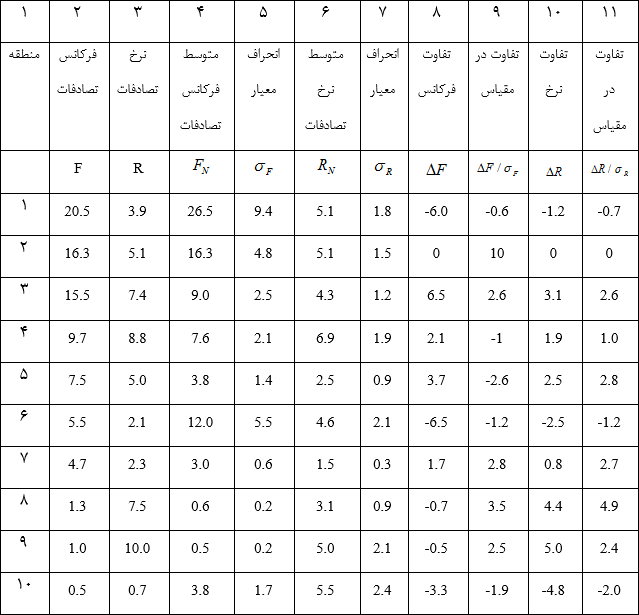
اطلاعات تصادفات به وقوع پیوسته در 10 منطقه در جدول 1 درج شده است. این 10 منطقه، به صورت نقطه ی ترافیکی مانند چهار راه یا مقاطعی با طول یکسان فرض شده اند. ستون دوم در جدول 1، فرکانس تصادفات در سال های گذشته را نمایش می دهد. در صورت اینکه فرکانس تصادفات را معیار قرار دهیم، مناطق 1، 2 و 3 به عنوان نقاط حادثه خیز انتخاب می شوند. این مناطق به احتمال فراوان به دلیل عبور و مرور زیاد دارای فرکانس تصادفات بالا می باشند، بنابراین اقدامات ایمن سازی چندان کارساز نخواهند بود.

تفاوت در مقیاس تفاوت نرخ تفاوت در مقیاس تفاوت فرکانس انحراف معیار متوسط نرخ تصادفات انحراف معیار متوسط فرکانس تصادفات نرخ تصادفات فرکانس تصادفات منطقه

ستون سوم در جدول 1، نرخ تصادفات را برای هر منطقه نمایش می دهد. در صورتی که نرخ تصادفات را معیار قرار دهیم، مناطق 4، 8 و 9 به عنوان مقاطع حادثه خیز شناسایی می شوند. همانطور که در جدول مشاهده می شود، مناطق 8 و 9 تعداد تصادفات کمی دارند و به دلیل عبور و مرور اندک دارای نرخ تصادفات بالا می باشند و در واقعیت انتخاب این مناطق برای ایمن سازی نمی تواند بازدهی مناسبی داشته باشد. به این نکته در شرح روش نرخ تصادفات نیز اشاره شد.
در روش کنترل کیفیت، مناطق مختلف بر اساس میزان ترافیک عبوری، وضعیت کنترل عبور و مرور، خصوصیات فیزیکی راه مانند قوس های افقی و قائم یا عرض مسیر و یا سایر خصوصیات، طبقه بندی می شوند. برای هر منطقه، متوسط فرکانس تصادفات و نرخ تصادفات در مناطق مشابه آن محاسبه شده و در ستون های 4 و 6 جدول 1 نمایش داده شده است. همین طور انحراف معیار فرکانس و نرخ تصادفات برای طبقه ی مربوط به هر منطقه، در ستون های 5 و 7 درج شده است. با در نظر گرفتن این پارامترها مشاهده می شود که با وجود اینکه منطقه ی 2 دارای فرکانس تصادفات بالا می باشد، ولی آمار یکسانی در مقایسه با مقاطع مشابه خود دارد. از سویی دیگر منطقه ی 5 آمار متناقضی نسبت به مقاطع مشابهش دارد، بنابراین حائز اهمیت بیشتری برای انتخاب به عنوان منطقه ی حادثه خیز و مستعد برای ایمن سازی، می باشد.
با در نظر گرفتن اختلاف فرکانس و نرخ تصادفات از میزان متوسط طبقه و مقایسه ی آن با انحراف معیار فرکانس و نرخ تصادفات در همان طبقه، مناطق حادثه خیز به روش کنترل کیفیت شناسایی می شوند. برای این منظور ستون های 9 و 11 در جدول 1 محاسبه شده است، این مقادیر از تقسیم اختلاف فرکانس و نرخ تصادفات میان هر منطقه با متوسط مورد نظر در همان طبقه بر انحراف معیار طبقه بر آورد شده اند. با در نظر گرفتن ستون های 9 و 11 منطقه ی 8 به عنوان منطقه ی حادثه خیز و مستعد برای ایمن سازی، به روش کنترل کیفیت شناسایی می شود. منطقه ی 8 دارای تعداد تصادفات بالاتر از مرزی است که برای مناطق مشابه آن در نظر گرفته شده، بنابراین با وجود اینکه در روش های فرکانس و نرخ تصادفات به عنوان نقطه حادثه خیز شناسایی نشده بود، در روش کنترل کیفیت به این عنوان شناسایی شد.

1-7 روش اندیس شدت(Severity Index Method)

در این روش به تصادفات جانی، جرحی و خسارتی وزن های متفاوتی نسبت داده شده و بر این اساس نقاط حادثه خیز مشخص می‌شوند (Kowtanapanich, 2007). اندیس شدت برای مقاطع مختلف جاده، مطابق با رابطه ی 2 محاسبه می شود.

در این رابطه SI اندیس شدت مقطع مسیر، وزن انواع تصادفات، K تعداد تصادفات جانی، A تعداد تصادفات جرحی درجه یک، B تعداد تصادفات جرحی درجه دو، P تعداد تصادفات خسارتی و T تعداد کل تصادفات می باشد.
هنگام استفاده از این روش باید دقت زیادی در تعیین اوزان مناسب برای انواع تصادفات نمود. اوزان تصادفات باید متناسب با زیان های اقتصادی و اجتماعی تصادفات مختلف تعیین گردد. به عنوان مثال Luathep زیان مالی تصادفات در یکی از ایالات تایلند را تعیین کرده و سپس نسبت تصادفات جانی، جرحی و خسارتی را برآورد نمود. در این تحقیق نهایتاً ضریب 125 برای تصادفات جانی، 9 برای تصادفات جرحی و 1 برای تصادفات خسارتی مد نظر قرار گرفت (Luathep & Tanaboriboon, 2005).

1-8 روش بایزین(Bayesian)

در روش های پیشین، تنها از سوابق تاریخی تصادفات برای شناسایی مقاطع حادثه خیز استفاده می شود. ضریب ایمنی مقاطعی از مسیر که دارای تصادفات زیاد در بازه ی زمانی کوتاهی می باشند، با دقت مناسبی از سابقه ی تاریخی تصادفات برآورد می شود. به عنوان مثال اگر در قسمتی از جاده به طور متوسط 100 تصادف در سال رخ دهد، با اطلاعات 3 سال تصادفات می توان فرکانس تصادفات را با انحراف معیار 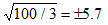برآورد نمود. ولی در مقاطعی از مسیر که تصادف به ندرت به وقوع می پیوندد، برآورد فرکانس تصادفات با خطای زیادی همراه می باشد. به عنوان مثال اگر در مقطعی از مسیر به طور متوسط در هر 10 سال 1 تصادف رخ دهد، انحراف معیار برآورد برابر با 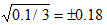خواهد بود. این در حالی است که متوسط وقوع تصادفات 1/0 بوده و انحراف معیار 18 برابر میانگین می باشد. بنابراین یکی از معایب روش هایی که تنها از سابقه ی تاریخی تصادفات برای تعیین میزان ایمنی یا ریسک قطعات مسیر استفاده می نمایند، کم دقت بودن این روش ها است (Hauer, Harwood, & Forrest, 2002).
استفاده از روش بایزین برای ارزیابی ضریب ایمنی قطعات مختلف جاده، می تواند دقت این ارزیابی را به میزان قابل توجهی افزایش دهد. این افزایش دقت ارزیابی به دلیل استفاده از دیگر منابع اطلاعاتی همراه با سابقه ی تاریخی تصادفات می باشد. در این روش از اطلاعات ایمنی برای مقاطع مشابه یک مقطع نیز در جهت برآورد ضریب ایمنی استفاده می شود. در ابتدا کلیاتی از تئوری بایزین مطرح شده و سپس نحوه ی استفاده از این تئوری در ارزیابی ایمنی تشریح می شود.

1-8-1 تئوری بایزین

تئوری بایزین از قانون ساده ای در مورد احتمال شرطی استفاده می نماید. احتمال شرطی یک متغیر مطابق با رابطه ی 3 تعریف می شود(Bolstad, 2004).

(3) 

با جایگذاری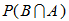 ، معادله ی 4 به دست می آید.

(4) 

رابطه ی 4 قانون بایزین را برای یک رخداد نمایش می دهد. در واقع قانون بایزین بیانی دیگر از احتمال شرطی می باشد. این قانون با یک مثال بهتر تشریح می شود. فرض کنید که یک کیسه ی پر از سکه داریم. 99% این سکه ها دارای یک پشت و یک رو و 1% باقیمانده دارای 2 رو می باشند. یک سکه از داخل کیسه برداشته شده و 3 بار پرتاب می گردد و در هر 3 بار روی سکه نمایان می شود. احتمال اینکه این سکه دارای 2 رو باشد چقدر است؟
محاسبه این احتمال بدون استفاده از قانون بایزین بسیار پیچیده است. ولی با استفاده از این قانون می توان فرض نمود که x متغیر تصادفی انتخاب شدن سکه ی دو رو و y متغیر تصادفی مربوط به آمدن 3 رو در 3 پرتاب باشد، در این صورت داریم:

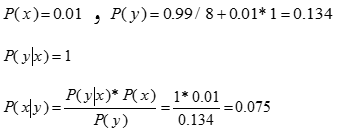
در این مثال احتمال اولیه ی انتخاب شدن یک سکه ی دو رو 1% می باشد، ولی با انتخاب یک سکه و سه بار مشاهده ی نتیجه ی پرتاب آن، احتمال ثانویه ی اینکه سکه دو رو بوده است از ترکیب احتمال اولیه ی آن و نتیجه ی آزمایش پرتاب سکه به دست می آید. مجموعاً در برخی مسائل، محاسبه احتمال x به شرط y بسیار مشکل بوده ولی احتمال y به شرط x به راحتی محاسبه می شود، در این گونه مسائل استفاده از قانون بایزین بسیار سودمند خواهد بود.
با نگاهی کلی تر به قانون بایزین مشخص می شود که در این قانون، احتمال ثانویه ی یک پدیده متناسب با احتمال اولیه آن و همچنین نتایج آزمایش های صورت گرفته، محاسبه می شود. در واقع می توان قانون بایزین را به صورت زیر بیان نمود(Bolstad, 2004).

(5) 

همانطور که در رابطه ی 5 نمایش داده شده است، در تئوری بایزین از نتایج مشاهدات انجام شده، احتمال یا دانش اولیه در مورد یک پدیده تکمیل شده و منجر به دستیابی به دانش ثانویه می شود.

1-8-2 کاربرد تئوری بایزین در شناسایی نقاط حادثه خیز

در شناسایی نقاط حادثه خیز با استفاده از روش بایزین، قطعات مختلف جاده ها بر اساس خصوصیات فیزیکی و ترافیکی مانند نوع جاده، عرض خط، میزان روشنایی، علامت گذاری ها، میزان ترافیک عبوری و … تقسیم بندی می شوند. برای هر قطعه از راه، مطابق با خصوصیات فیزیکی یا ترافیکی آن، ضریب ایمنی اولیه ای در نظر گرفته می شود. این ضریب ایمنی می تواند مطابق با خصوصیات آن قطعه، و یا از آمار تصادفات در قطعات مشابه، محاسبه شود. سپس از آمار تصادفات در آن قطعه از مسیر نیز استفاده شده و ضریب ایمنی نهایی محاسبه می شود. در واقع در این روش مطابق با نوع هر قطعه از جاده، دانش اولیه ای برای ضریب ایمنی آن وجود دارد. سپس از تصادفات صورت گرفته در آن قطعه مانند آنچه در روش بایزین نتایج آزمایش نام برده شد، استفاده شده و دانش ثانویه ای برای ضریب ایمنی یک قطعه از مسیر به دست می آید.
جهت ارزیابی ایمنی جاده ها توسط تئوری بایزین، دو روش مورد استفاده قرار گرفته است:
1- بایزین تجربی(Empirical Bayesian)
2- بایزین کامل(Full Bayesian)

1-8-3 بایزین تجربی

استفاده از روش بایزین تجربی برای برآورد ضریب ایمنی قطعات یک مسیر شامل 5 مرحله می باشد(Powers & Carson, 2004):
1- برآورد توابع عملکرد ایمنی((Safety Performance Function (SPF)
2- محاسبه پارامتر پراکندگی(Overdispersion parameter)
3- محاسبه اوزان نسبی
4- برآورد ضریب ایمنی نهایی
5- محاسبه ی واریانس برآورد ضریب ایمنی
نحوه ی انجام این مراحل در ادامه شرح داده شده است.

1-8-3-1 برآورد توابع عملکرد ایمنی

مرحله ی اول در فرآیند تعیین ضرایب ایمنی با استفاده از روش بایزین تجربی، برآورد توابع عملکرد ایمنی می باشد. تابع عملکرد ایمنی، یک مدل ریاضی است که احتمال وقوع تصادف در یک قطعه از مسیر را برآورد می نماید. بنابر تحقیقات انجام گرفته توسط Hauer، احتمال وقوع تصادف به بهترین شکل توسط یک تابع آماری چند متغیره، مدل سازی می شود. این تابع می تواند یک معادله ی ساده برای مرتبط ساختن احتمال وقوع تصادفات و خصوصیات قابل اندازه گیری راه ها مانند میزان ترافیک عبوری، طول قطعه، عرض خط عبوری، عرض شانه ی راه و … باشد (Powers & Carson, 2004). رابطه ی 6 بیانگر یک تابع عملکرد ایمنی خطی می باشد.

در این رابطه :
میزان برآورد برای ضریب ایمنی قطعه ی i ( تعداد تصادفات در قطعه i )
تا پارامترهای قابل برآورد
تا متغیر های مستقل مانند متوسط ترافیک روزانه، تعداد خطوط، عرض خط، محدودیت سرعت و …
می باشند .
تابع عملکرد ایمنی جاده، از داده های جمع آوری شده برای تصادفات و شرایط وقوع آن ها در منطقه ی مورد مطالعه برآورد شده و پس از آن می تواند برای تخمین میزان ایمنی مقاطع مختلف راه مورد استفاده قرار گیرد.

1-8-3-2 محاسبه ی پارامتر پراکندگی
مقادیر محاسبه شده از توابع عملکرد ایمنی، با استفاده از روش های آماری کالیبره می شوند. در فرآیند کالیبراسیون، معمولاً توزیع تصادفات را به صورت توزیع دوجمله ای منفی در نظر می گیرند. یکی از پارامترهای این توزیع پارامتر پراکندگی می باشد. این پارامتر برای قطعات یک مسیر به ازای طول واحد مسیر محاسبه می شود. این پارامتر از رابطه ی 7 محاسبه می شود (Hauer, et al., 2002).

(6) 

در این رابطه :

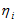 میزان برآورد برای ضریب ایمنی قطعه ی i ( تعداد تصادفات در قطعه i )

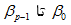 پارامترهای قابل برآورد

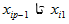 متغیر های مستقل مانند متوسط ترافیک روزانه، تعداد خطوط، عرض خط، محدودیت سرعت و …  می باشند .

تابع عملکرد ایمنی جاده، از داده های جمع آوری شده برای تصادفات و شرایط وقوع آن ها در منطقه ی مورد مطالعه برآورد شده و پس از آن می تواند برای تخمین میزان ایمنی مقاطع مختلف راه مورد استفاده قرار گیرد.

1-8-3-2 محاسبه ی پارامتر پراکندگی

مقادیر محاسبه شده از توابع عملکرد ایمنی، با استفاده از روش های آماری کالیبره می شوند. در فرآیند کالیبراسیون، معمولاً توزیع تصادفات را به صورت توزیع دوجمله ای منفی در نظر می گیرند. یکی از پارامترهای این توزیع پارامتر پراکندگی(Overdispersion) می باشد. این پارامتر برای قطعات یک مسیر به ازای طول واحد مسیر محاسبه می شود. این پارامتر از رابطه ی 7 محاسبه می شود (Hauer, et al., 2002).

(7)

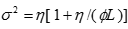
 که در این رابطه:

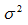 واریانس تعداد تصادفات در قطعات هم نوع از شبکه ی راه ها

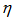  تعداد تصادف مورد انتظار که از توابع عملکرد ایمنی برای هر قطعه با طول L و در بازه ی زمانی Y محاسبه می شود

L طول قطعه

  پارامتر پراکندگی

می باشند. از این رابطه در جهت برآورد پارامتر پراکندگی استفاده می شود. از این پارامتر در مرحله ی بعد برای محاسبه اوزان مربوط به توابع عملکرد ایمنی و آمار تصادفات استفاده می شود.

1-8-3-3 محاسبه ی اوزان نسبی

در این مرحله به مقادیر به دست آمده از توابع عملکرد ایمنی و اطلاعات آمار تصادفات، وزن اختصاص داده می شود تا با استفاده از این اوزان برآورد نهایی برای ضریب ایمنی هر قطعه از مسیر انجام پذیرد. وزن مربوط به مقدار به دست آمده از تابع عملکرد ایمنی از رابطه 8 محاسبه می شود(Hauer, et al., 2002).

(8)

که در این رابطه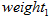 ، وزن محاسبه شده برای برآورد تابع عملکرد ایمنی، 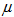تعداد تصادفات مورد انتظار برآورد شده از تابع عملکرد ایمنی برای یک سال، Y بازه ی زمانی بر حسب سال که اطلاعات تصادفات آن در محاسبات وارد می شود و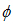پارامتر پراکندگی می باشد. همین طور وزن اطلاعات تصادفات خود مقطع از رابطه ی 9 محاسبه می شود. در رابطه ی 9،  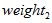وزن مربوط به اطلاعات تصادفات می باشد.

(9)

ربا نگاهی اجمالی به این رابطه نمایان می شود که با افزایش بازه زمانی اطلاعات تصادفات یک مقطع، میزان وزن محاسبه شده برای تابع عملکرد ایمنی کاهش یافته و وزن بیشتری به اطلاعات تصادفات همان مقطع نسبت می یابد.

1-8-3-4 برآورد ضریب ایمنی نهایی

پس از محاسبه ی وزن ها، مقادیر ضریب ایمنی به سادگی و با تلفیق نتایج تابع عملکرد ایمنی و تصادفات یک قطعه محاسبه می شوند. برای محاسبه ی ضریب ایمنی یک قطعه از رابطه ی 10 استفاده می شود(Hauer, et al., 2002).

(10)

در رابطه ی 10
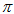ضریب نهایی برآورد شده برای هر قطعه
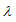میزان متوسط تعداد تصادفات برای هر قطعه
می باشد. سایر پارامتر های این رابطه پیشتر شرح داده شده اند.

1-8-3-5 محاسبه ی واریانس ضریب ایمنی

مقدار نهایی ضریب ایمنی، عددی میان برآورد تابع عملکرد ایمنی و متوسط تصادفات می باشد. واریانس محاسبه ی ضریب ایمنی مطابق با رابطه ی 11 برآورد می شود.

(11)

پس از طی این مراحل، فرآیند برآورد ضریب ایمنی به انجام می رسد. در تحقیقات گذشته، مدل های متنوعی با تغییرات جزیی در فرآیند ذکر شده، ارائه شده اند. در برخی مدل ها به جای تابع عملکرد ایمنی، متوسط تعداد تصادفات در مقاطع مشابه مورد استفاده قرار گرفته است. در این صورت برآورد ضریب ایمنی از رابطه ی 12 صورت می پذیرد.

(12)

در این رابطه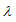مقدار متوسط تصادفات در قطعه ی مورد نظر و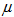متوسط تعداد تصادفات در قطعات مشابه می باشد. مقدار وزن نیز از رابطه ی 13 بر آورد می شود.

(13)

در رابطه ی 13،انحراف از معیار در تعداد تصادفات در قطعات مشابه،انحراف از معیار در تعداد تصادفات به صورت سالیانه در همان قطعه و n بازه زمانی داده ی تصادفات بر حسب سال می باشد.

تیم ایده نگاروندا